Batch 2 - Class 283 - Behavioral Economics III, Walter's Magical Squares

• Can you tile a 6x6 grid with 2x1 dominos, so that there are no fault lines (i.e. any horizontal or vertical line has at least one dominos going across it?)
• Answer: Can't be done - each of 10 lines in 6x6 grid divides the region into two even areas, so at least two dominoes must cross it. So there must be at least 20 dominoes, but there are only 18

• Double the Pot - Each person got five coins and could contribute any number to a doubling pot. While classical economics nash equilibrium for this is that no one should contribute anything, people continue to contribute
• Marginal value of gains and losses are different, and this produces risk aversion
• Sunk Costs - while classical economics says that sunk costs should be ignored, humans demonstrate endowment effect and assign value to sunk costs

• Suppose we play a game of proposers and responders. So the proposer gets Rs 100 and can make an offer to share part of this with the responder. If the responder declines, none of the players get anything. If the responder agrees, they split the money as proposed. 
• Let's play this game, and see what happens. If we don't get enough spread, let everyone respond to "What's the minimum amount at which you would accept?" without knowing the proposed amount.
• What is the "rational" strategy? The proposer should offer Rs 1, and the responder should agree to it
• What did we observe
• Did all proposers offer Rs 1? If not, why not?
• Did responders accept any amount they were offered? Why not?
• Both these have to do with our sense of fairness - both for proposer and for responders
• Lets explore this a bit more. Uber does surge pricing. 
• How many people think that surge pricing is fair? To what extent of surge?
• Suppose there is a emergency (a fire). Do you think surge pricing is fair in that circumstance? How much? Do you think the cab drivers feel that surge pricing is fair in that case? 
• Suppose you were told that 30% of the surge proceeds go to a charity. Do you think its fair now with the purpose?
• Suppose you understood that in a high-traffic situation, there is more fuel burn and hence higher cost of operation. Do you think its fair now that it is linked to the cost itself?
• How would you use the above behavioral insights in deciding price increases for your favorite food item?

• Let kids come up with a 3x3 magic square

• Let kids play the game a few times
• What if the numbers are, or are not, restricted to 1-9?
• What if you put identical numbers on your square corners?
• What if you put very different numbers on your corners (like 1, 100, 10000 and 1 million)?
• Is there a "best" strategy? How would you play?

• (Dudeney - 230) Here is a pretty little puzzle that only requires twelve pennies or counters. Arrange them in a circle, as shown in the illustration. Now take up one penny at a time and, passing it over two pennies, place it on the third penny. Then take up another single penny and do the same thing, and so on, until, in six such moves, you have the coins in six pairs in the positions 1, 2, 3, 4, 5, 6. You can move in either direction round the circle at every play, and it does not matter whether the two jumped over are separate or a pair.

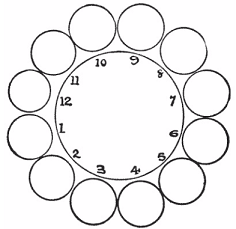
• Answer: 12->3, 7->4, 10->6, 8->1, 9->5, 11->2
• What if we wanted them to jump two stacks of pennies, regardless of number of pennies in that stack?
• Answer: 10->1, 9->6, 11->2, 8->5, 12->3, 7->4